

# those formula at specific numeric value of p. # small imaginary artefacts produced when evaluating
# Extra precision is taken, to try and deal with # for the eigenvalues, in terms of parameter p # This produces R, as explicit symbolic formulas restart Ĭp := collect(cp/lambda^2,lambda,factor): Here is revised code, with the now symmetric Matrix k. These need not produce nonzero imaginary component artefacts as noise due to roundoff error. It thus still may be superior to use a dedicated root-finder on the characteristic polynomial, or compute the eigenvalues numerically, following substitution at floating-point values of parameter p. Note however that these involve radicals and the imaginary unit, and immediate substitution of a floating-point value for parameter p results in small nonzero imaginary component in the results (as numeric roundoff artefact). This results in 8 explicit formulas (in terms of parameter p) for the eigenvalues. That also allows the characteristic polynomial of the exact rational form of k+kG to factor symbolically w.r.t. Following clarification by the Original Poster I make an adjustment below to replace the former definition of the entry of Matrix k by the value for its entry. Is that intentional, or a mistake? (If k is intended to be symmetric then please clarify, because it means that k+kG can be cast as a Maple Matrix with shape=symmetric and the floating-point eigenvalue computation will be a little faster, produce no 0.0*I imaginary artefacts, and return sorted by default.) Then, we compute the covariance matrix of the data and calculate the eigenvalues and corresponding eigenvectors of this covariance matrix. I could mention that kG is symmetric, and k is almost symmetric. KG := p/840*Matrix(,Ĭp := CharacteristicPolynomial(Q, lambda):Ĭp := lambda^2*collect(cp/lambda^2,lambda,factor)
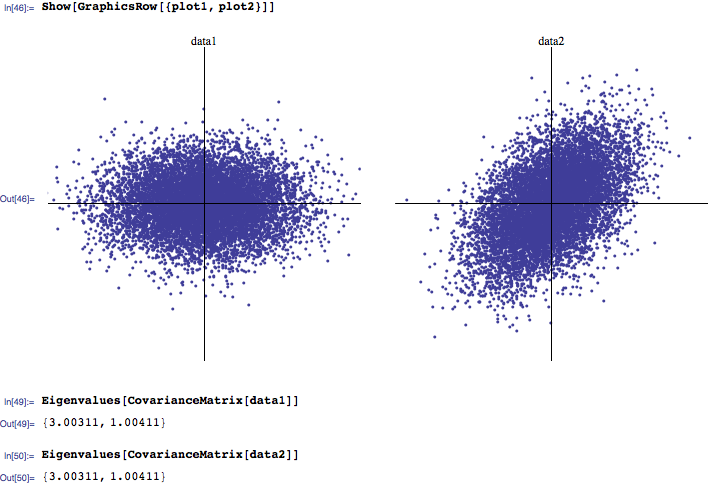
CALCULATE FIRST 10 EIGENVALUES MATLAB CODE
Perhaps the following code will help get you started. So you will need to substitute numeric values for p, in order to obtain the remaining eigenvalues as floating-point. If you convert all your floating-point coefficients to exact rationals then it appears that k+kG has eigenvalue zero with multiplicity of two.īut the characteristic polynomial that remains (after dividing out lambda^2) is of degree 6, and that does not appear to factor directly. In order to find the time interval, we first need to determine the damped period of the system. I heard maple can solve this problem but I am amateur on maple. Note To request eigenvectors, and in all other cases, use eigsto find the eigenvalues or eigenvectors of sparse matrices. d eig(A,B) returns a vector containing the generalized eigenvalues, if Aand Bare square matrices. The "Arnoldi" method is also known as a Lanczos method when applied to symmetric or Hermitian matrices.I have a problem to calculate eigenvalues of a symbolic matrix. Description d eig(A) returns a vector of the eigenvalues of matrix A.Explicit Method settings for approximate numeric matrices include:Īrnoldi iterative method for finding a few eigenvaluesĭirect banded matrix solver for Hermitian matricesĭirect method for finding all eigenvaluesįEAST iterative method for finding eigenvalues in an interval (applies to Hermitian matrices only ).Whether to use radicals to solve quartics Eigenvectors has the following options and settings:.SparseArray objects and structured arrays can be used in Eigenvalues.Eigenvalues ] gives k eigenvalues, or as many as are available.Eigenvalues is always equivalent to Take, spec ].
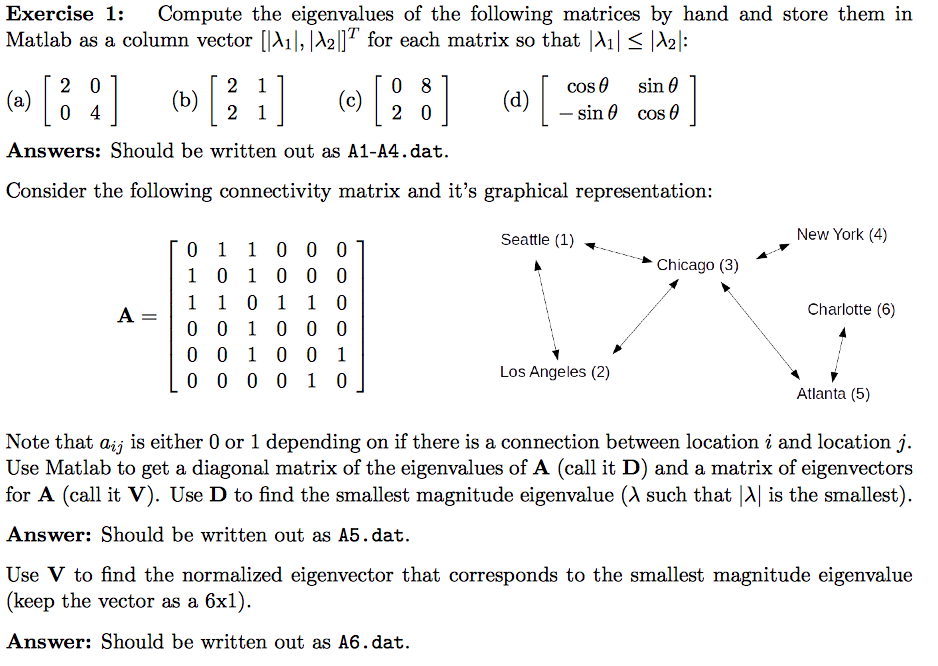
Eigenvalues gives the k that are smallest in absolute value. The greedy approach to find the best fit 2-dimensional subspace for a matrix A, takes v1 as the first basis vector for the 2-dimenional subspace and finds the.For numeric eigenvalues, Eigenvalues gives the k that are largest in absolute value.When matrices m and a have a dimension ‐ shared null space, then of their generalized eigenvalues will be Indeterminate.
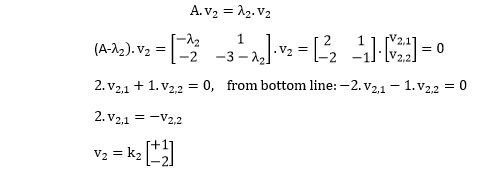


 0 kommentar(er)
0 kommentar(er)
